Surfing Troves: Integral transform

Mathematical notation aside, the motivation behind integral transforms is easy to understand. There are many classes of problems that are difficult to solve—or at least quite unwieldy algebraically—in their original representations. An integral transform "maps" an equation from its original "domain" into another domain. Manipulating and solving the equation in the target domain can be much easier than manipulation and solution in the original domain. The solution is then mapped back to the original domain with the inverse of the integral transform.

Table of integral transforms
Transform	Symbol	$K$	t₁	t₂	$K - 1$	u₁	u₂
Fourier transform	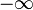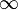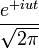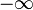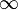$\mathcal{F}$	$\frac{e^{-iut}}{\sqrt{2 \pi}}$	$-\infty\,$	$\infty\,$	$\frac{e^{+iut}}{\sqrt{2 \pi}}$	$-\infty\,$	$\infty\,$
Fourier sine transform	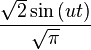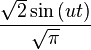$\mathcal{F}_s$	$\frac{\sqrt{2}\sin{(ut)}}{\sqrt{\pi}}$	$0\,$	$\infty$	$\frac{\sqrt{2}\sin{(ut)}}{\sqrt{\pi}}$	$0\,$	$\infty$
Fourier cosine transform	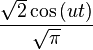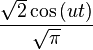$\mathcal{F}_c$	$\frac{\sqrt{2}\cos{(ut)}}{\sqrt{\pi}}$	$0\,$	$\infty$	$\frac{\sqrt{2}\cos{(ut)}}{\sqrt{\pi}}$	$0\,$	$\infty$
Hartley transform	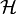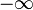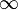$\mathcal{H}$	$\frac{\cos(ut)+\sin(ut)}{\sqrt{2 \pi}}$	$-\infty\,$	$\infty\,$	$\frac{\cos(ut)+\sin(ut)}{\sqrt{2 \pi}}$	$-\infty\,$	$\infty\,$
Mellin transform	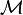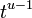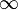$\mathcal{M}$	$t^{u-1}\,$	$0\,$	$\infty\,$	$\frac{t^{-u}}{2\pi i}\,$	$c\!-\!i\infty$	$c\!+\!i\infty$
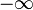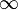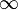Two-sided Laplace transform	$\mathcal{B}$	$e^{-ut}\,$	$-\infty\,$	$\infty\,$	$\frac{e^{+ut}}{2\pi i}$	$c\!-\!i\infty$	$c\!+\!i\infty$
Laplace transform	$\mathcal{L}$	$e^{-ut}\,$	$0\,$	$\infty\,$	$\frac{e^{+ut}}{2\pi i}$	$c\!-\!i\infty$	$c\!+\!i\infty$
Weierstrass transform	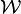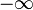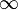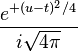$\mathcal{W}$	$\frac{e^{-(u-t)^2/4}}{\sqrt{4\pi}}\,$	$-\infty\,$	$\infty\,$	$\frac{e^{+(u-t)^2/4}}{i\sqrt{4\pi}}$	$c\!-\!i\infty$	$c\!+\!i\infty$
Hankel transform		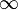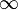$t\,J_\nu(ut)$	$0\,$	$\infty\,$	$u\,J_\nu(ut)$	$0\,$	$\infty\,$
Abel transform		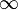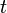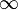$\frac{2t}{\sqrt{t^2-u^2}}$	$u\,$	$\infty\,$	$\frac{-1}{\pi\sqrt{u^2\!-\!t^2}}\frac{d}{du}$	$t\,$	$\infty\,$
Hilbert transform	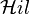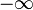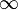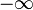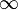$\mathcal{H}il$	$\frac{1}{\pi}\frac{1}{u-t}$	$-\infty\,$	$\infty\,$	$\frac{1}{\pi}\frac{1}{u-t}$	$-\infty\,$	$\infty\,$
Poisson kernel		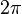$\frac{1-r^2}{1-2r\cos\theta +r^2}$	$0\,$	$2\pi\,$
Identity transform		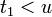$\delta (u-t)\,$	$t_1<u\,$	$t_2>u\,$	$\delta (t-u)\,$	$u_1\!<\!t$	$u_2\!>\!t$

In the limits of integration for the inverse transform, c is a constant which depends on the nature of the transform function. For example, for the one and two-sided Laplace transform, c must be greater than the largest real part of the zeroes of the transform function.

Although the properties of integral transforms vary widely, they have some properties in common. For example, every integral transform is a linear operator, since the integral is a linear operator, and in fact if the kernel is allowed to be a generalized function then all linear operators are integral transforms (a properly formulated version of this statement is the Schwartz kernel theorem).
The general theory of such integral equations is known as Fredholm theory. In this theory, the kernel is understood to be a compact operator acting on a Banach space of functions. Depending on the situation, the kernel is then variously referred to as the Fredholm operator, the nuclear operator or the Fredholm kernel.

Surfing Troves

Welcome

Disclaimer

Monday, December 20, 2010

Integral transform

No comments:

GoogleAds